Définition / Méthode de recherche
Cercle - Ellipse
Cercle - Ovale


  Définition :
On dénomme surface dite "composée", le solide dont la surface latérale est constituée de plusieurs éléments, ces éléments étant une partie de surface développable tel que ( plan, cylindre , cône, etc...)


  Plans tangents:
La recherche des plans tangents délimitant la surface latérale entre deux sections dans 2 plans parallèles est la méthode choisie pour définir notre surface composée.



La recherche des plans tangents dans la pratique se limite dans le cas des bases parallèles à trouver le minimum de plans (tangents aux 2 sections à raccorder) déterminant des surfaces planes de raccordement
Ceci nous amène à tracer 2 droites parallèles tangentes respectivement aux 2 sections à raccorder en s'appuyant sur les droites existantes des sections

Dans le cas présent , nous tracerons 3 droites tangentes à la section circulaire respectivement parallèles aux 3 segments de droites AB, BC, CD.


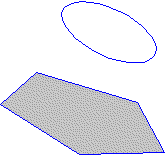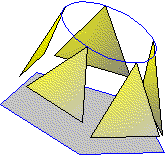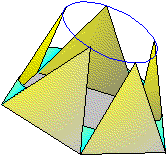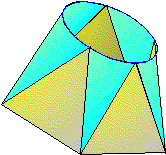
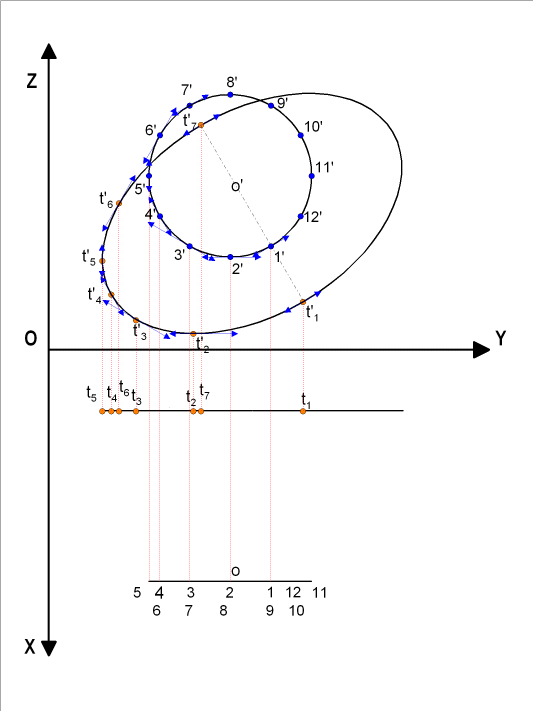
Raccordement d'un cercle et d'une ellipse

Dans cet exemple, il n'y aucune partie droite sur les 2 sections à raccorder, nous avons donc à rechercher des droites (génératrices) qui définiront notre raccord.

  • Commençons par déterminer un nombre de points sur le cercle ( 12 pour ce cas) mais notre travail va se limiter à la moitié puisque le solide possède un plan de symétrie.
  • En PF, prenons le point (2'), traçons une tangente au cercle en ce point.
  • puis traçons une tangente à l'ellipse parallèle à la tangente au point (2'), ce qui détermine le point (t2')
  • procédons pour l'ensemble des autres points ce qui nous donnent une succession de points de tangence sur l'ellipse( t'3, t'4, t'5, t'6, t'7 ) puis par rappel en PH
  • Après avoir tracé les génératrices reliant les 2 sections (1A, 2B, 3C, 4D, 5E, 6F, 7G), il nous faut tracer des "diagonales" ( 2A, 3B, 4C, 5D, 6E, 7F) pour nous permettre d'établir le développement.

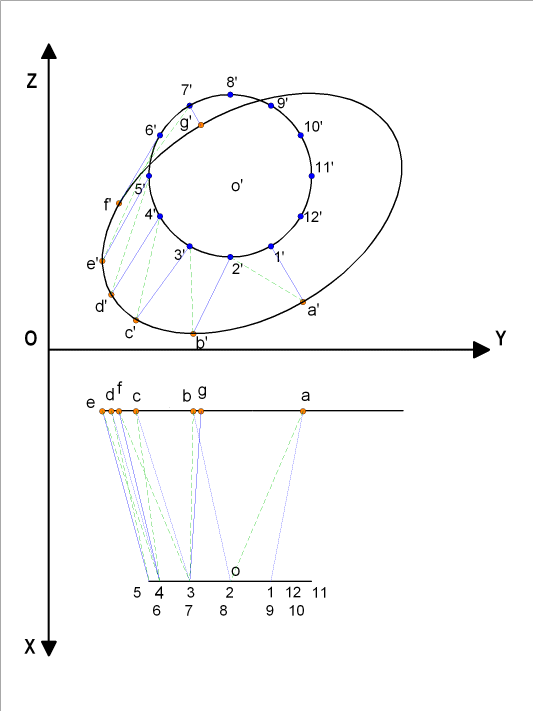
Attention si ces " diagonales " appartiennent à l'enveloppe de notre raccord, ce ne sont pas des droites mais des courbes. Il est important de bien garder cela à l'esprit lors du développement. Il faut éviter un trop grand écart entre la longueur droite et la longueur courbe.

Il est évident que ces "diagonales" , telles qu'elles sont représentées, n'appartiennent pas à l'enveloppe. Notre erreur dans le développement sera minime si ces "diagonales" ne s'éloignent pas de trop de l'enveloppe.
La recherche des vraies grandeurs des génératrices et "diagonales" se fait par la méthode "géométrique"( : projection frontale des droites et différence d'éloignement )
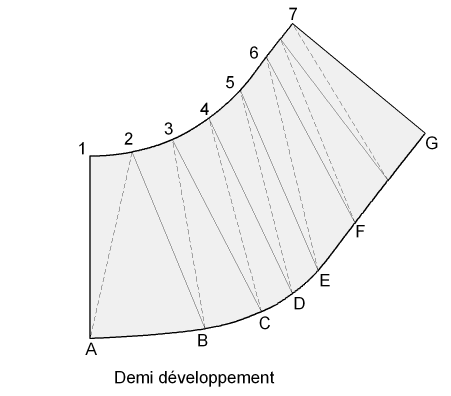
Pour le développement, nous portons la valeur de la corde entre le point ( a ) et le point ( b ) en PH de l'ellipse en sachant que ceci est théoriquement une erreur mais ne pouvons pas non plus porter la valeur de courbe.
Il faut pratiquement contrôler la transformée de la courbe à chaque 1/4 de l'ellipse et rectifier si nécessaire par rapport à la valeur calculée au préalable.Une génératrice supplémentaire entre bles points F et G apporte une plus grande précision au tracé



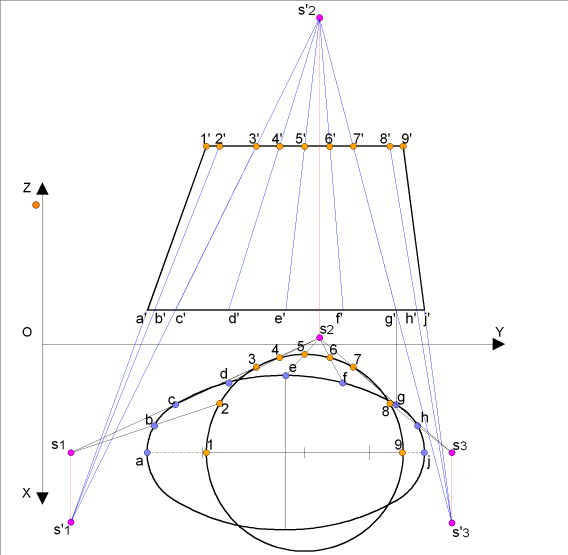
Raccordement d'un cercle et d'un ovale

Dans cette situation

  • il convient de chercher le plan tangent à chaque point de raccordement de l'ovale [ovale type anse de panier] ( T1, T2, T3, T4 ), ce qui donnent respectivement les points ( G 1,G2, G3, G 4) sur le cercle, délimitant les surfaces de raccordement qui dans ce cas sont des surfaces tronconiques puisque les rayons sont différents

  • le tracé fait apparaître 4 surfaces tronconiques de sommets (S1, S2, S3, S4 ),
  • nous choisissons de diviser nos bases en un nombre de génératrices
    • tantôt sur le cercle
    • tantôt sur l'ovale pour éviter de trop grand écart au pied de certaines génératrices
  • le solide présente un axe de symétrie ce qui nous autorise à ne recherche qu'un demi développement

 

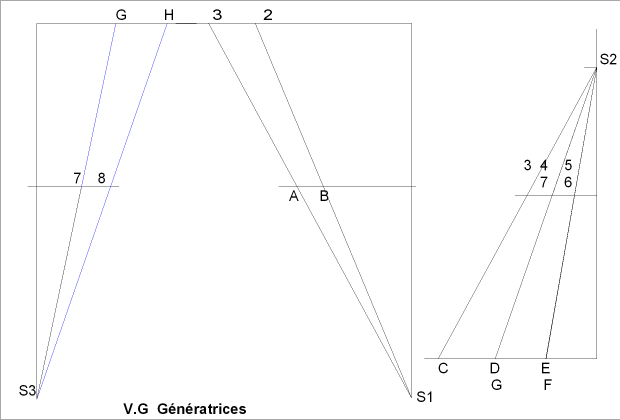La recherche des vraies grandeurs des génératrices des surfaces tronconique se fait par la méthode "géométrique":( projection horizontale des droites et différence de cotes)

Notre surface présente un plan de symétrie, nous permettant un demi développement. nous portons la valeur de la corde entre le point (1) et le point (2) en PH du cercle en sachant que ceci est est théoriquement une erreur mais ne pouvons pas non plus porter la valeur de courbe.

Il faut pratiquement contrôler la transformée de la courbe à chaque 1/4 de l'ellipse et rectifier si nécessaire par rapport à la valeur calculée au préalable.
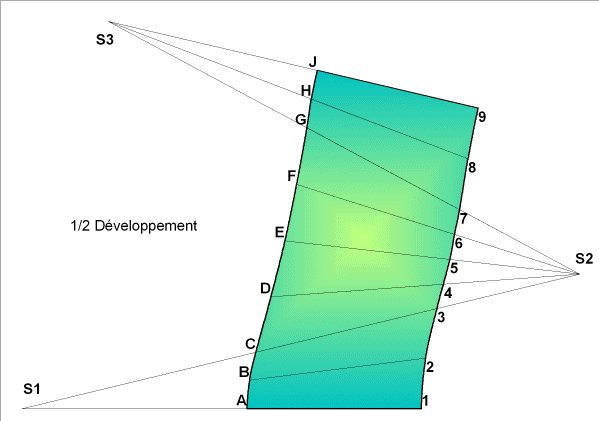