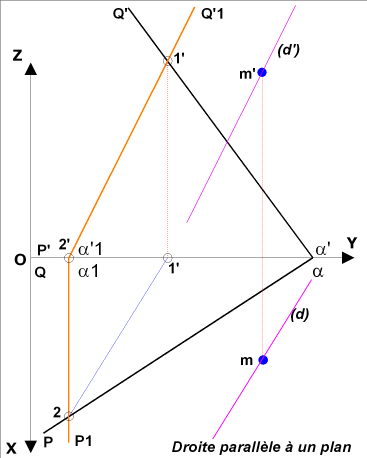
Leurs intersections avec un troisième
donnent 2 droites parallèles
Pour faciliter les recherches
nous déterminerons les intersections avec les plans
particuliers perpendiculaires aux plans de projection
Animation
d'une intersection droite et plan
|
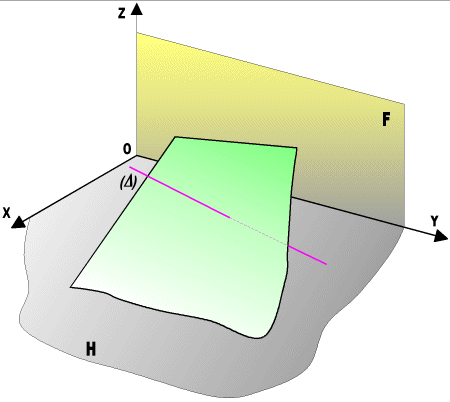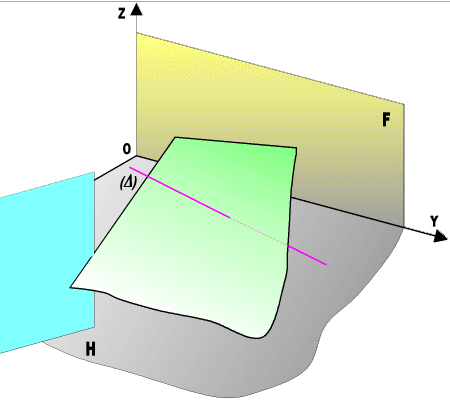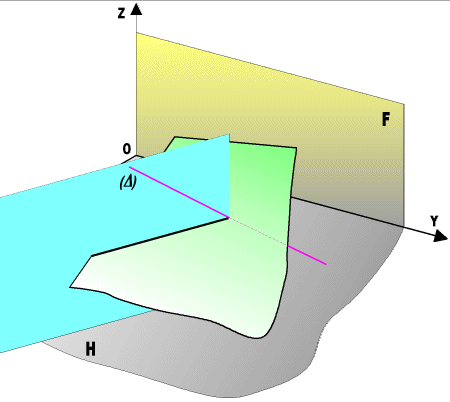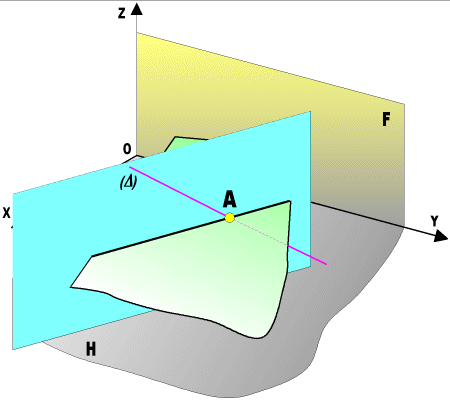 |
Intersection plan quelconque
et plan vertical
Prenons un plan quelconque P et un plan vertical V définis
par leurs traces PaQ' et VbS'
|
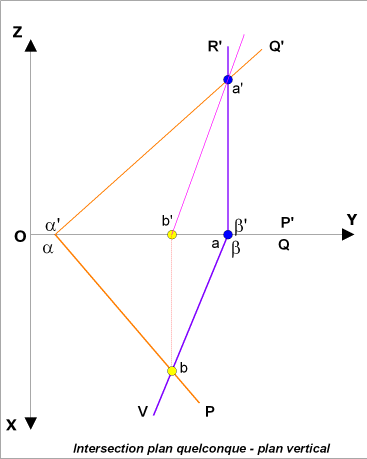
Nous remarquons :
- que leurs traces respectives se coupent en 2 points A( a,
a') et B (b, b')
qui représentent la droite
d'intersection des 2 plans P et V
- que la projection horizontale de
la droite (ab) est bien confondue
avec la trace horizontale du plan vertical Vb
|
 |
Intersection
plan quelconque et plan de bout
Prenons un plan quelconque P défini par 2 droites D et D sécantes
et un plan de bout P1 défini par ses traces PaQ'
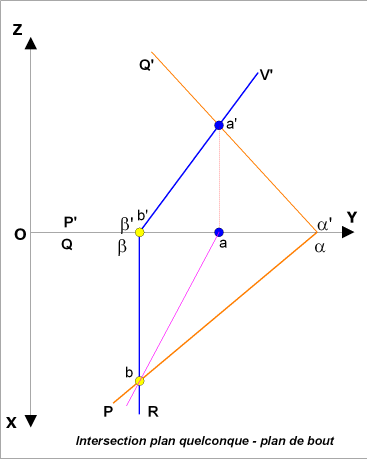 |
Nous remarquons :
- que la trace frontale du plan de bout P1 coupe la droite D au
point A( a, a') et la
droite D au point B (b,
b') qui représentent la droite
d'intersection des 2 plans P et P1
- que la projection frontale de
la droite (a'b') est bien confondue
avec la trace frontale du plan de bout a Q'
|
Intersection
d'une droite et d'un plan
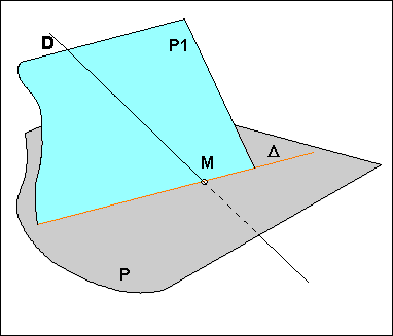
| Pour déterminer l'intersection
d'une droite D et d'un plan P , il suffit de rechercher
l'intersection d'un plan auxiliaire P1 passant
par la droite avec le plan P |
 |
|
Exemple : Soit un plan P défini
par 3 points A,B,C et une droite MN
Prenons un plan auxiliaire particulier
(vertical ) passant par
la droite D et coupant le plan ABC suivant la droite MN
- le plan auxiliaire V (PaQ' )
coupe le plan ABC en projection horizontale suivant la droite 1-2 (1 Î AC et 2 Î BC )
ce qui donne la projection frontale des 2 points par ligne de rappel
( 1' et 2' )
- la droite 1'2' coupe la droite MN (mn, m'n')
au point J (j',j) point
d'intersection de la droite et du plan
|
 |
Intersections
de 2 plans quelconques
|
Supposons que 2 plans P et P1 se coupent, leur intersection
est une droite MN, il suffit donc de:
- rechercher 2 points communs aux 2 plans pour résoudre le
problème.
- le point M recherché sera
obtenu par l'intersection des 2 droites (D1, D1) Þ résultantes
de l'intersection d'un plan auxiliaire R avec les plans P et P1
- le point N par l'intersection
des 2 droites (D2 ,D2) Þ résultantes
de l'intersection d'un plan auxiliaire R1 avec les plans P et P1
|
 |
Nous n'allons pas traiter toutes les formes de représentation des plans
mais une seule plus courante en traçage
Les surfaces planes sont définies par 3
points A,B,C (triangle) et par 2
droites parallèles formant un parallélogramme D,E,F,G
Plusieurs solutions s'offrent à nous dans le choix des plans
auxiliaires, nous avons moins de constructions en utilisant
un plan auxiliaire passant par une droite définissant l'un des
plan
Prenons comme plan auxiliaire,
le plan
de bout
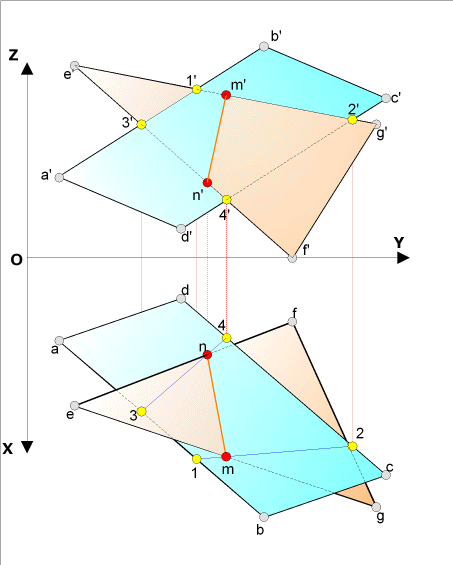
Soit le plan
de bout P1 passant par la droite EG du plan EFG et
le plan de bout P2 passant par la droite EF du plan EFG
En projection frontale
- l'intersection entre
le plan P1 et le plan ABCD donne la droite (1'2')
- l'intersection entre
le plan P2 et le plan ABCD donne la droite (3'4')
En projection horizontale
- par ligne
de rappel nous obtenons les points
( 1 ) sur (ab),
( 2 )
sur (cd ), ( 3
) sur (ab) et ( 4
) sur (cd).
- traçons les droites (12) et
(34) ,
ces droites coupent respectivement pour (12) Þ (eg)
ce qui donne le point ( m ),
et pour ( 34) Þ ( ef )
ce qui donne le point ( n)
- par ligne de rappel en projection F, nous trouvons les
points ( m' ) sur ( e'g')
et ( n') sur ( e'f')
La droite MN est donc la droite
d'intersection entre les plans ABCD et EFG
|
 |

![]()
![]()