Détermination / Trace horizontale / Trace frontale /
Types de plan / Droites du plan

 

Détermination du plan 
Nous pouvons déterminer un plan par:

•

3 points non alignés ( Fig. 1)

•

1 droite et un point hors droite ( Fig. 2)

•

2 droites sécantes ( Fig. 4) ou parallèles ( Fig. 3)

Pour simplifier l'étude du plan, nous utilisons 2 droites sécantes ou parallèles pour matérialiser nos plans (les 2 premiers modes de représentation pouvant se ramener au troisième ou quatrième)

  
Traces d'un plan: ( vidéo)

Trace horizontale:

On appelle trace horizontale d'un plan la droite suivant laquelle le plan rencontre le plan horizontal de projection. Cette trace est le lieu des points du plan de cote nulle, donc pour définir cette droite il suffit de chercher les traces horizontales de 2 droites du plan

En projection frontale •   nous recherchons les points des droites de cotes nulles (a' pour la droite D et b' pour la droite D ) •   droite ( a',b' ) Þ projection frontale de la trace horizontale du plan En projection horizontale •   par lignes de rappel, on obtient le point ( a ) sur la droite D et ( b ) sur la droite D •   droite ( a,b ) Þ  projection horizontale de la trace horizontale du plan

Par convention la trace horizontale est dénommée Pa , P'a'

Trace frontale:

On appelle trace frontale d'un plan la droite suivant laquelle le plan rencontre le plan frontal de projection. Cette trace est le lieu des points du plan d'éloignement nul, donc pour définir cette droite il suffit de chercher les traces frontales de 2 droites du plan

En projection horizontale •   nous recherchons les points des droites d'éloignement nul (b pour la droite D et a pour la droite D ). •   droite ( a,b ) Þ  projection horizontale de la trace frontale du plan En projection frontale •   par lignes de rappel, on obtient le point ( b' ) sur la droite D et ( a' ) sur la droite D •   droite ( a',b'  )Þ projection frontale de la trace frontale du plan

Par convention la trace frontale est dénommée Qa, Q'a'

Les traces d'un plan définissent parfaitement celui-ci et sa notation abrégée est PaQ'

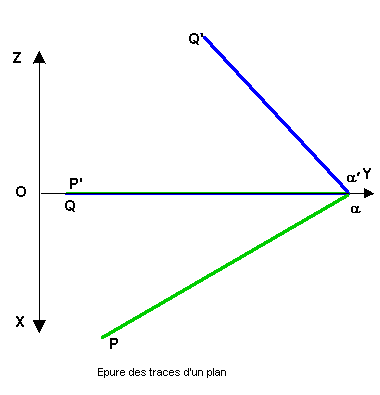Attention: les traces sont deux droites distinctes du plan leur intersection étant le point (a,a' ) confondu avec la ligne de terre

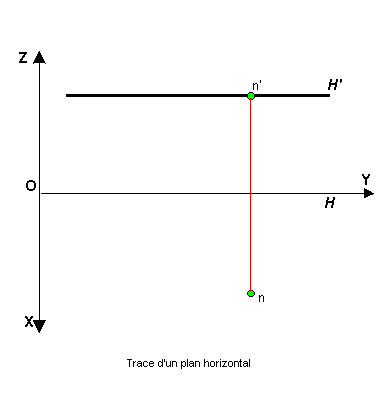
Plan horizontal : plan parallèle au plan horizontal de projection

•

il n'a qu'une trace frontale symbolisée par H H'

Plan horizontal en perspective

Pour qu'un point N appartienne au plan H, il suffit •   qu'il se distribue ( n' ) sur la projection H' de la trace frontale du plan

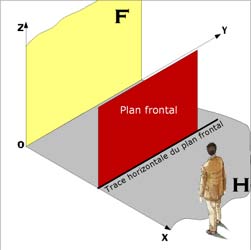
Plan frontal : plan parallèle au plan frontal de projection

•

il n'a qu'une trace horizontale symbolisée par F F'

Plan frontal en perspective

Pour qu'un point N appartienne au plan F il suffit •   qu'il se distribue ( n ) sur la projection F de la trace horizontale du plan

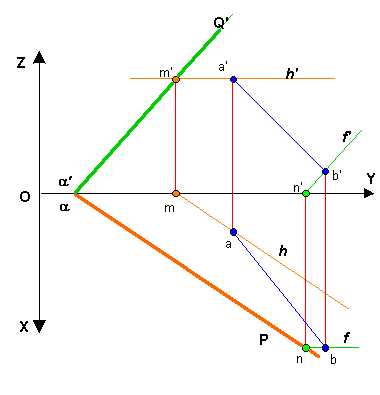
Plan vertical : plan perpendiculaire au plan horizontal de projection. Sa trace frontale a'Q' est perpendiculaire à la ligne de terre Y'OY.

Plan vertical en perspective

L'épure du plan vertical ci-contre montre les traces du plan ainsi que 2 points distincts M et N •   le point M appartient au plan vertical car sa projection horizontale ( m) est confondue avec la projection horizontale de la trace horizontale du plan (Pa) •   le point N n'appartient pas au plan vertical puisque ( n ) n'est pas confondu avec la projection horizontale de la trace horizontale du plan(Pa )

Plan de bout : plan perpendiculaire au plan frontal de projection. Sa trace horizontale Pa est perpendiculaire à la ligne de terre Y'OY.

Plan de bout en perspective

L'épure du plan de bout ci-contre montre les traces du plan ainsi que 2 points distincts M et N •   le point N appartient au plan de bout car sa projection frontale ( n') est confondue avec la projection frontale de la trace frontale du plan (a'Q'). •   le point M, il n'appartient pas au plan de bout puisque ( m' ) n'est pas confondu avec la projection frontale de la trace frontale du plan (a'Q').

NB. Il est bon de bien connaître ces plans car il nous permettent par la suite de nombreuses résolutions de problèmes de traçage.

Nous n'avons pas volontairement désigné le   plan de profil ( plan perpendiculaire à la ligne de terre) comme un plan particulier puisque au contraire des précédents, il n'offre pas davantage ( souvent traité avec un changement de plan ou rabattement)

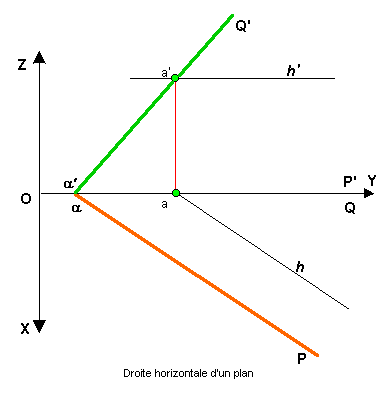
Droites horizontales : Les horizontales d'un plan sont les droites d'intersection de ce plan avec les plans horizontaux, ce qui fait que ces droites sont parallèles entre elles (ch. droite) . Les projections H et F d'une horizontale d'un plan seront parallèles aux traces de même nom du plan

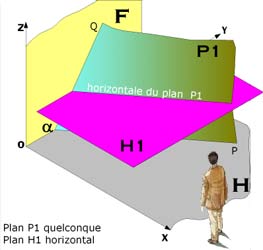Dans l'exemple ci-contre la droite H est définie par sa projection frontale ( h') •   elle coupe la trace frontale (aQ, a 'Q' ) au point A (a, a') •   il suffit de tracer la projection horizontale ( h) droite parallèle à la projection horizontale de la trace horizontale ( Pa )

Droites frontales : Les frontales d'un plan sont les droites d'intersection de ce plan avec les plans frontaux, ce qui fait que ces droites sont parallèles entre elles (ch. droite) Les projections H et F d'une frontale d'un plan seront parallèles aux traces de même nom du plan

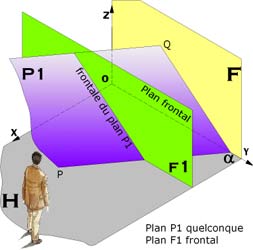Dans l'exemple ci-contre la droite F est définie par sa projection horizontale ( f ) •   elle coupe la trace horizontale( Pa, P'a ' ) au point B (b, b') •   il suffit de tracer la projection frontale (f') droite parallèle à la projection frontale de la trace frontale (a 'Q' )

Droites quelconques : Pour qu'une droite appartienne à un plan il suffit que 2 points de cette droite soient dans ce plan. Une solution consiste à utiliser les droites particulières du plan (frontale ou horizontale )

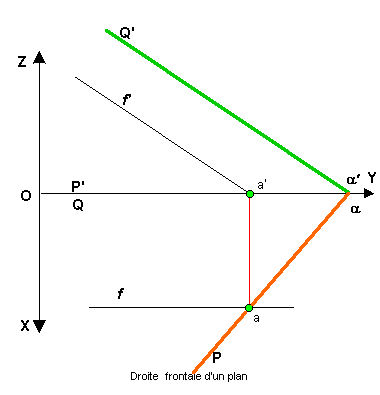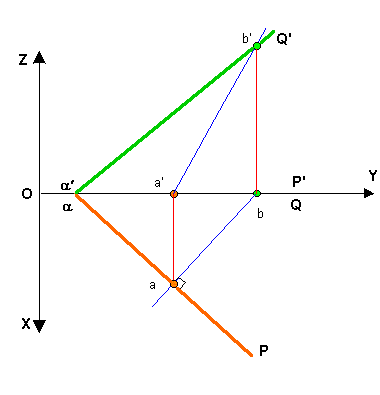
Le plan est défini par ses traces( PaQ' ) et la droite par sa projection frontale (a'b'). •   pour déterminer la projection horizontale (ab) de la droite , nous faisons passer une droite horizontale du plan ( h ,h') par le point A ce qui définit un point M (m,m') intersection avec la trace frontale du plan Þ (a) situé sur ( h ) •   pour changer faisons passer une droite frontale du plan (f,f' ) par le point B ce qui définit un point N ( n,n' ) intersection avec la trace horizontale du plan Þ ( b) situé sur ( f ) voir vidéo

•   Tracer la projection horizontale de la droite ( ab ) perpendiculaire à la projection horizontale de la trace horizontale (Pa ) qui détermine 2 points d'intersection (a,b) en projection H •   puis par lignes de rappel les projections (a', b' ) définissant la projection frontale de la ligne de plus grande pente