Untitled Document

Principe / Rabattement d'un plan sur le plan H / Rabattement d'un point / Homologie / Rabattement d'un plan

Principe
L'étude du rabattement permet d'amener une figure plane dans une position particulière par rapport aux plans de projection.

Animation d'un rabattement d'une droite AB dans un plan horizontal

Rabattement d'un plan sur le plan horizontal
Nous nous contenterons d'étudier le rabattement sur le plan horizontal mais toute la stratégie peut s'appliquer au rabattement sur le plan frontal .
Le rabattement d'un plan P sur un plan horizontal est le procédé qui consiste à faire tourner ce plan autour d'une de ces droites pour le positionner tel qu'il soit parallèle ou confondu au plan horizontal
La charnière sera toujours une droite horizontale du plan donné ( droite d'intersection entre du plan horizontal et plan à rabattre)

Pendant le rabattement du plan autour de la charnière horizontale H

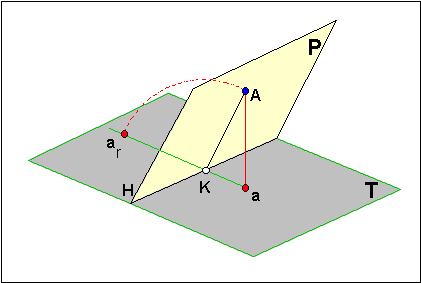le point A décrit un arc de cercle dans un plan perpendiculaire à la droite H passant par le point K

On a donc :

KA = KA'

aKAr Þ droite perpendiculaire à H

aA est la différence de cotes entre le point A et le plan horizontal
ce qui nous conduit à la règle du triangle rectangle

Rabattement d'un point :

Règle du triangle rectangle
Le rabattement d'un point:

a lieu sur la perpendiculaire menée de la projection horizontale du point sur celle de la charnière

à une distance de cette charnière égale à l'hypoténuse d'un triangle rectangle dont les cotés de l'angle droit sont :

la distance entre les projections horizontales du point et de la charnière

la différence de cotes entre le point et la charnière

Soit le point A (a, a') et l'horizontale H (h, h') prise comme charnière qui définisse un plan P

par le point (a ) en projection horizontale menons une perpendiculaire à ( h) qui nous donne le point (k )
construire le triangle rectangle angle droit en ( a ) et porter sur ce coté de l'angle droit la différence de cotes entre (a') et la droite ( h')
puis par le point ( k) comme centre et ( k ar) comme rayon décrire l'arc de cercle qui définit la position du point ( a1 ) rabattement du point A par rapport à H .
L'angle ( a ) étant l'angle en VG des 2 plans , tous les triangles rectangles de rabattement sont semblables

Loi d'homologie

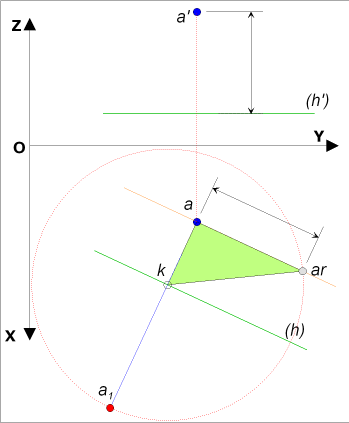Le rabattement d'un point et sa projection horizontale sont sur une même perpendiculaire à la projection horizontale de la charnière

La projection horizontale d'une droite et son rabattement coupent la projection horizontale de la charnière au même point

Rabattement d'un plan quelconque:

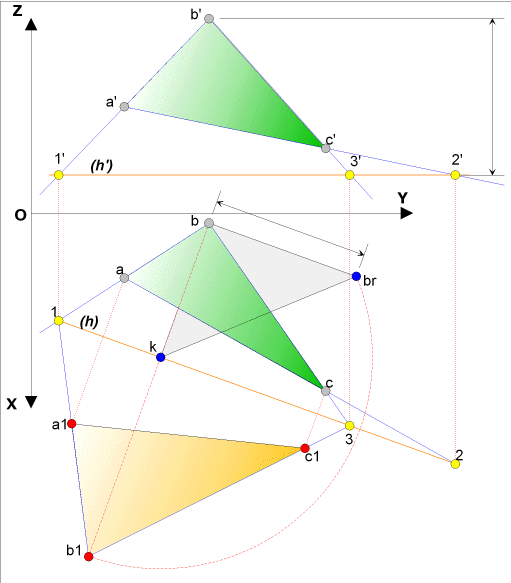
Soit un triangle ABC défini par ses projections frontale et horizontale exécutons un rabattement

Choisissons une horizontale H (h,h') du plan ABC ce qui nous donnent les points 1(1,1') , 2 (2, 2'), 3(3,3')
puis du point (b ) en projection horizontale, nous déterminons la perpendiculaire à ( h) et le triangle rectangle de rabattement (bkbr) en PH où(bbr = différence de cote entre l'horizontale et le point B)
Obtention du point (b₁) par rabattement du point (br) avec le point (k )comme centre ainsi que des points (a₁) et (c₁) par construction et ligne de rappel

voir animation