![]()
![]()
Nous sommes souvent amenés à déterminer la vraie grandeur de l'angle de 2 surfaces planes présentées sous diverses formes et diverses projections ( hotte , prisme , pyramide , surface composée, etc.)
Nous vous proposons quelques solutions qui permettent de définir la vraie
grandeur de l'angle de pliage appelé aussi rectiligne
du dièdre
Dans le cas d'une surface prismatique , la recherche de la vraie grandeur de
la section
normale est la vraie grandeur
de l'ensemble des angles de pliage pour le formage de cette surface.
Solution
changement de plan
Pour voir notre angle de pliage en VG, il suffit que
les 2 points formant
l'arète soient confondus dans
une projection, ce qui nous conduit à transformer une droite (quelconque
, frontale ou horizontale) en une droite ( de bout ou verticale )
|
Cette solution permet de définir la VG de l'angle de
pliage quelque soit la position des plans constituant l'angle à
déterminer ( angle suivant la droite BE )
|
 |
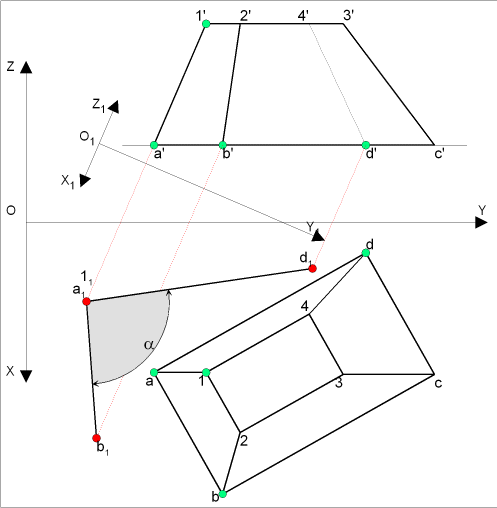 |
Recherche de l'angle suivant la droite A1
|
|
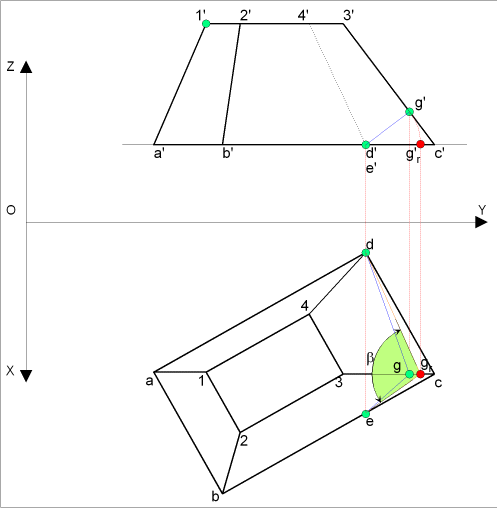
Recherche de l'angle suivant la droite C3
|
 |
|
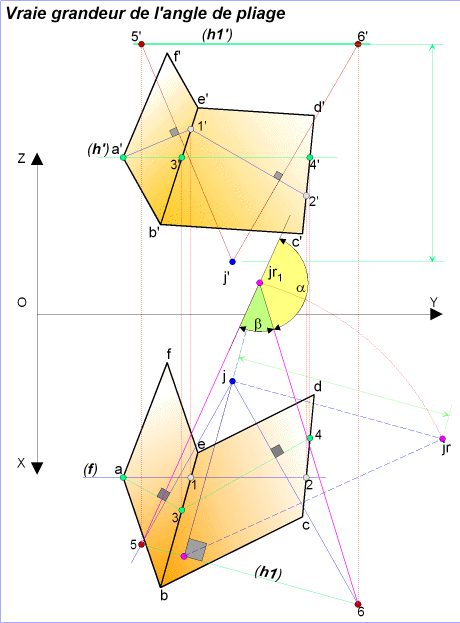
Recherche de l'angle suivant la droite BE
|
 |