Définition / Méthode de recherche


Cercle Polygone rayons
Cercle - Polygone
Cercle - Polygone rayons
Cercle - Polygone rayons
Cercle - Polygone
Cercle - Polygone rayons


  Définition :
On dénomme surface dite "composée", le solide dont la surface latérale est constituée de plusieurs éléments, ces éléments étant une partie de surface développable tel que ( plan, cylindre , cône, etc...)



  Plans tangents:
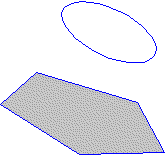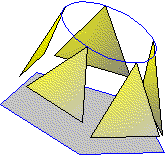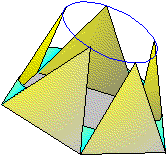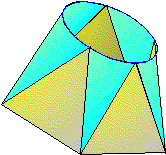
La recherche des plans tangents délimitant la surface latérale entre deux sections dans 2 plans parallèles est la méthode choisie pour définir notre surface composée.

Pour voir l'animation ci-dessous faire un clic droit puis sur Lire



La recherche des plans tangents dans la pratique se limite dans le cas des bases parallèles à trouver le minimum de plans (tangents aux 2 sections à raccorder) déterminant des surfaces planes de raccordement
Ceci nous amène à tracer 2 droites parallèles tangentes respectivement aux 2 sections à raccorder en s'appuyant sur les droites existantes des sections

Dans le cas présent , nous tracerons 3 droites tangentes à la section circulaire respectivement parallèles aux 3 segments de droites AB, BC, CD.


   Raccordement d'un cercle et d'une section avec rayons

Il faut commencer par déterminer les surfaces planes de raccordement

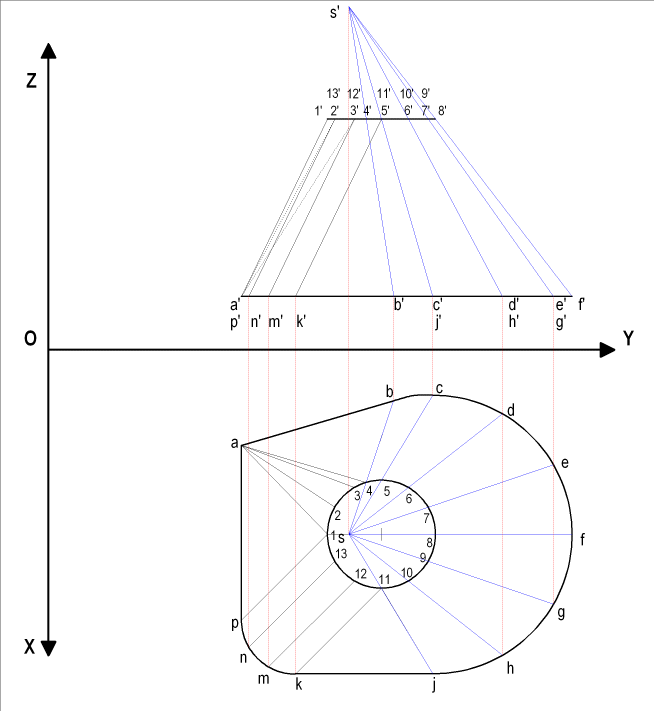  • en PH , traçons une perpendiculaire, à chacun des segments de droite définissant la section ( polygone avec rayons),passant par le centre du cercle, ce qui donnent 3 points (t1, t2,t3) sur le cercle en projection horizontal et par ligne de rappel (t'1, t'2, t'3) en projection frontale
  • nous voyons apparaître 3 plans triangulaires et entre chaque des surfaces diverses ( portion de cône dit oblique, portion de tronc de cône et portion de cylindre dit oblique)
Il convient de tracer un nombre de génératrices pour déterminer ainsi nos diverses surfaces
  • Portion de cône oblique ( A1,A2,A3,A4)
  • Portion de tronc de cône oblique( S4B,S5C,S6D,S7E,S8F,S9G,S10H,S11J)
  • Portion de cylindre (K1,M11,N12,P13)
 
  • la partie cylindrique nous amène à effectuer un changement de type frontal (OX1,OY1,OZ1)
  • plaçons OY1 parallèle aux génératrices (PH ) de la portion cylindrique pour nous donner les vraies grandeurs des génératrices
  • ainsi définissons la vraie grandeur de la section normale (m2,n2,p2,q2) (Voir Cylindre oblique)
  • la recherche des vraies grandeurs des génératrices des surfaces conique et tronconique se fait par la méthode "géométrique": projection horizontale des droites et différence de cotes
  • pour le développement, nous partageons la surface en 2 parties,avec comme lignes d'assemblage la génératrice F8 et la droite perpendiculaire issue du point (1 ) dans le plan AQ1

Nous avons volontairement fait ce demi développement en tracé intérieur (voir tracé intérieur)

Nous avons volontairement fait ce demi développement en tracé extérieur(voir tracé extérieur)

 


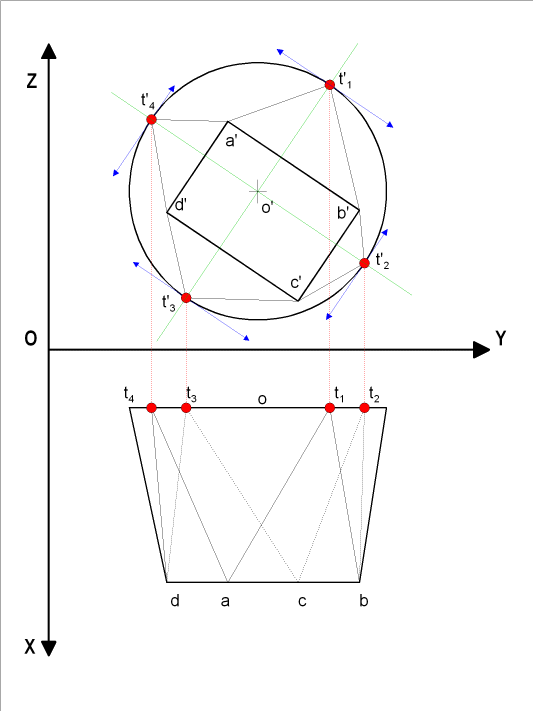
   Raccordement d'un cercle et d'un rectangle

 

Il faut commencer par déterminer les surfaces planes de raccordement

  • traçons une perpendiculaire en PF, à chacun des segments de droite définissant la section rectangulaire, passant par le centre du cercle, ce qui donnent 4 points (t'1, t'2,t'3,t'4) sur le cercle en projection frontale et par ligne de rappel (t1, t2, t3,t4) en PH
  • Nous voyons apparaître 4 plans triangulaires et entre chaque des surfaces (portion de cône dit oblique)
 
Il convient de tracer un nombre de génératrices pour déterminer ainsi nos diverses surfaces
  • Portion conique (AT4,A1,A2,A3,AT1)
  • Portion conique (AT1,B4,B5,B6,BT2)
  • Portion conique (CT2,C7,C8,C9,CT3)
  • Portion conique (DT3,D10,D11,D12,DT4)

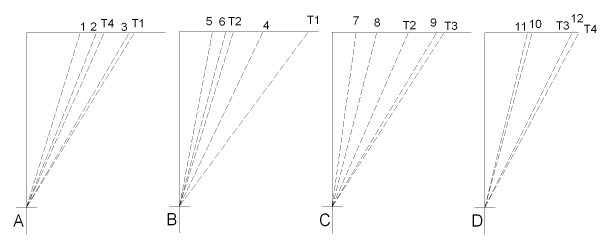
La recherche des vraies grandeurs des génératrices des surfaces coniques se fait

  • par la méthode"géométrique" projection frontale des droites et différence d'éloignement


Pour le développement, nous partageons la surface en 2 parties,avec comme lignes d'assemblage :

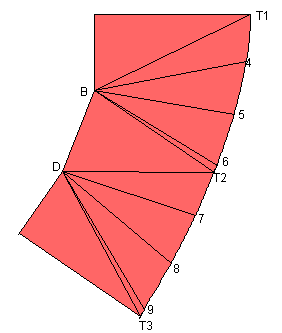  • la droite perpendiculaire issue du point T1 dans le plan ABT1
  • la droite perpendiculaire issue du point T3 dans le plan CDT3 (voir tracé intérieur)

  



Comme dans tous les développements de pièce il est bon de contrôler les transformées des courbes si possible , dans le cas ci-dessus , la longueur totale de la courbe est égal à :

L =P x diamètre


   Raccordement d'un cercle et d'un polygone avec rayons

L'exemple ci-contre reprend pratiquement tous les exemples précédents de la page mais il faut être vigilant lorsque les courbes d'une base ne sont pas tangentes aux rayons ( exemple au point A)

  • Le plan tangent passant par la droite AB donne un point de contact sur le cercle au point ( 2 ) Þ plan tangent ( AB2)
  • au point A le plan tangent , dont la trace avec plan frontal passant par la base mixte (polygone avec rayons) est tangente au rayon , donne sur le cercle un point de tangence en (1), faisant apparaître une portion de surface conique de sommet A et de base 1-2.

Nous n'avons pas effectuer le développement, celui-ci étant similaire au cocktail des précédents de la page.