Analytique / Rotation / Géométrique / Changement de plan / Rabattement

En traçage, il faut porter sur les développements les vraies grandeurs des droites définissant l'enveloppe. Il convient donc de connaître les diverses possibilités de recherches de la vraie grandeur de la droite.( Par commodité VG signifie vraie grandeur)
 
  

Solution analytique
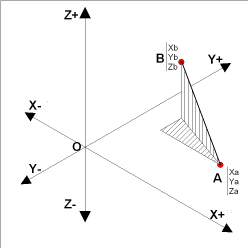
Considérons une droite AB définie par les coordonnées cartésiennes de ses points A (XA,YA, ZA) et B (ZB,YB, ZB), la valeur de sa vraie grandeur est donnée par:

(VG AB)² = (XA-XB)² + (YA-YB)² +(ZA-ZB)²

  
Solution par rotation
Une droite étant en vraie grandeur lorsqu'elle est parallèle à un plan de projection , il faut donc transformer une droite quelconque en droite particulière

Exemple 1 : transformons la droite AB par rotation en une droite frontale.

Par le point A provoquons une rotation telle que le point B ait le même éloignement que le point A En projection horizontale ( XA = XB ) Þ ( m a) = ( m br) En projection frontale •   les cotes de A et de B restent inchangées Þ ( ZB ) =(ZBr) La droite (a' br') représente la vraie grandeur de AB

Par le point B provoquons une rotation telle que le point A ait la même cote que le point B En projection frontale ( ZA = ZB ) Þ ( m ar') = ( m b) En projection horizontale •   les éloignements de A et de B restent inchangés Þ ( XA) =(XAr)   La droite (ar b) représente la vraie grandeur de AB

Dans l'exemple 1, la VG de la droite est l'hypoténuse d'un triangle rectangle dont les 2 cotés de l'angle droit sont respectivement égal à :

Pour trouver la VG de la droite: Il suffit de tracer deux droites perpendiculaires et de porter sur les cotés de l'angle droit respectivement les valeurs: ( ab) Þ projection horizontale de la droite (ZB-ZA) Þ différence de cotes entre les 2 points

Dans l'exemple 2, la VG de la droite est l'hypoténuse d'un triangle rectangle dont les 2 cotés de l'angle droit sont respectivement égal à :

• ( XB-XA ) Þ différence d'éloignements entre A et B
• ( a' br' ) = ( a'b') Þ projection frontale de la droite

Pour trouver la VG de la droite: Il suffit de tracer deux droites perpendiculaires et de porter sur les cotés de l'angle droit respectivement les valeurs: ( a'b') Þ projection frontale de la droite (XB-XA) Þ différence d'éloignements entre les 2 points

 

Nous retrouvons dans ces 2 solutions la formule analytique puisque la VG de la droite est l'hypoténuse du triangle rectangle dont les 2 cotées de l'angle droit sont :

premier cas :

ZA - ZB et ab or (ab)² = ( XA -XB )² + (YA - YB)²

deuxième cas :

XA - XB et a'b' or (a'b')²= ( ZA -ZB )² + (YA - YB)²

  
Solution par changement de plan de projection

Animation de la vraie grandeur de la droite par changement de plan frontal de projection

Il faut choisir un nouveau plan de projection judicieux tel que la droite devienne parallèle à ce plan, il en existe n soit horizontaux soit frontaux

Choisissons un référentiel (O₁X₁,O₁Y₁,O₁Z₁) telle que la droite O₁Y₁ soit parallèle ou confondue à la projection ( horizontale de la droite ou frontale de la droite)
 

Cas du plan horizontal : La droite devient horizontale puisque ( Z1A ) = ( Z1B) voir vidéo

Cas du plan frontal : La droite devient frontale puisque ( X1A) = ( X1B)

  
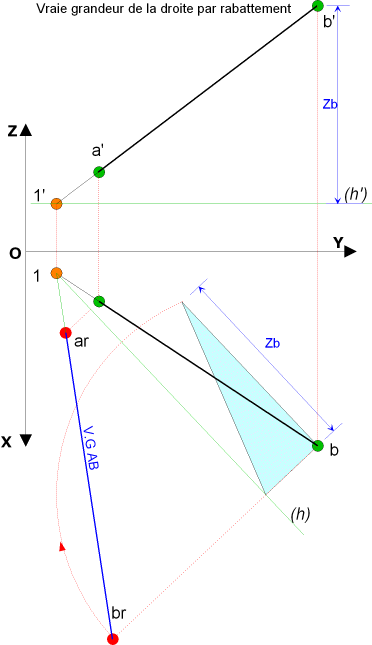
Solution par rabattement:

Soit la droite définie (ab, a'b') déterminons une droite horizontale telle qu'elle forme un plan avec la droite AB Þ point (1, 1') commun aux 2 droites effectuons un rabattement autour de ( h, h' ) de la droite (ab, a'b') qui place la droite en VG Pour faciliter le rabattement nous pourrions choisir la droite horizontale passant par le point (a,a' )

Le choix de la recherche varie suivant le nombre de droites à rechercher ; dans le cas de solides à droites parallèles le changement de plan sera plus judicieux par contre la rotation conviendra mieux aux surfaces coniques avec sommet, la solution géométrique n'encombrant pas l'épure semble la plus judicieuse.