Principe / Droite axe vertical / Droite axe de bout / Plan quelconque / Cas particulier

Principe  
Un point M tourne autour d'un axe D, il décrit un cercle :

 
  Pour exécuter des rotations nous avons intérêt à choisir comme axes de rotation des droites soient de bout soient verticales afin que les cercles décrits se projettent en V.G sur l'une des projections

  
Rotation d'une droite autour d'un axe vertical


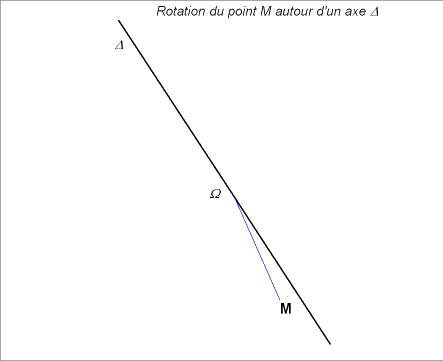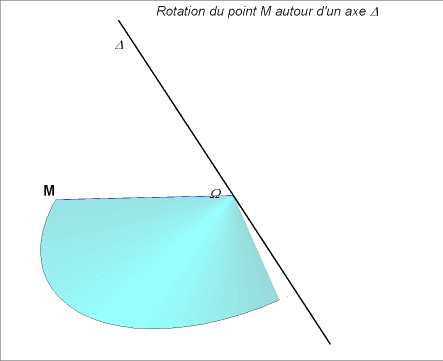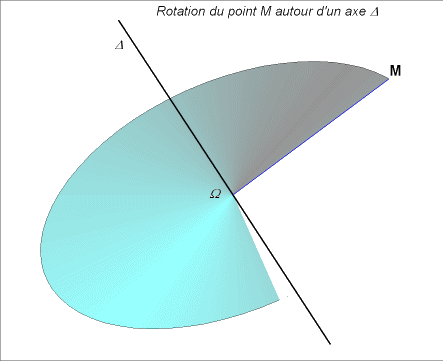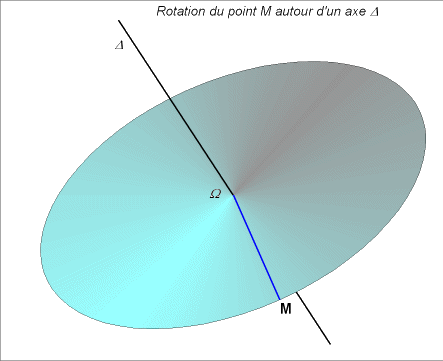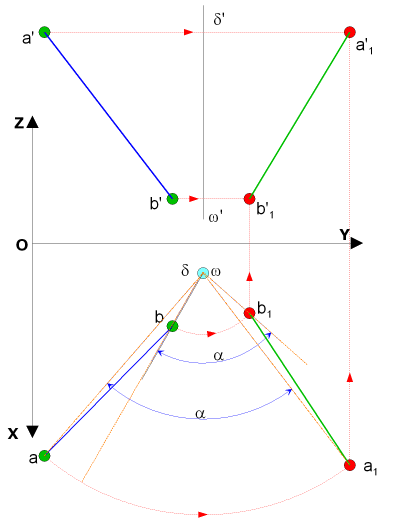
La droite AB décrit une rotation d'un angle ( a ) autour d'un axe vertical W D

En projection horizontale

les points ( a ) et ( b ) décrivent des arcs de cercle de centre ( w ) jusqu'en ( a1 ) et ( b1)

En projection frontale
  • les points ( a' ) et ( b' ) se déplacent parallèlement à OY en ( a'1 ) et ( b'1) obtenus par ligne de rappel
Pour diminuer les constructions il serait bon de choisir un point particulier de la droite, le point K qui sera le pied de la perpendiculaire commune à la droite et à l'axe
 
  
Rotation d'une droite autour d'un axe de bout

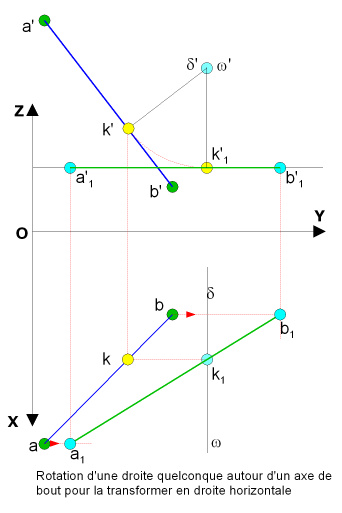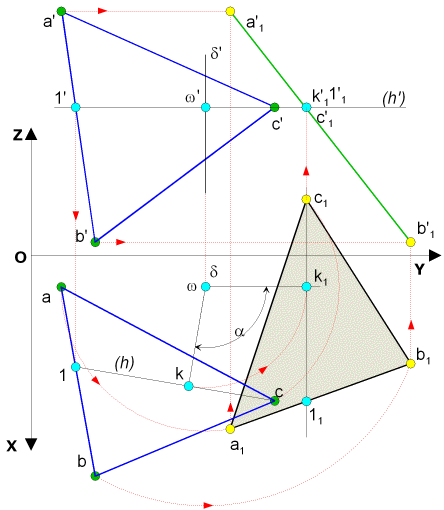
Dans cette exemple la droite AB est quelconque

  • on choisit un axe D de bout et l'on recherche le point K tel que ( k' ) soit sur le cercle tangent à la projection ( a'b' de la droite (w'k' ) est le rayon du cercle de la rotation )
  • pendant la rotation, la droite reste toujours tangente au cercle lorsque qu'elle est parallèle à la ligne de terre nous cessons la rotation,définissant les points ( a'1 et ( b'1)
  • par ligne de rappel nous trouvons la projection horizontale ( a1 b1 )

    la droite ( a1 b1) est la V.G de la droite AB




   
Rotation d'un plan ABC autour d'un axe vertical

En projection horizontale

  • de l'axe de rotation D et de la droite ( wk) (rayon du cercle tangent à la droite( h ) comme rayon nous exécutons la rotation jusqu'à ce que la droite ( h) devienne une droite de bout , c'est à dire perpendiculaire au plan frontal de projection soit en projection horizontale perpendiculaire à OY ,( ceci nous definit une valeur angulaire a )
  • nous déterminons les autres points (a1,b1 c1) du plan par rotation à la valeur angulaire a.

En projection frontale

  • les points se déterminent par ligne de rappel nous constatons que l'ensemble des points ( a'1 , b'1, c'1, k'1 , 1'1 ) sont sur la même ligne , notre triangle est devenu un plan de bout
    voir vidéo



Par des constructions similaires avec un axe de bout, nous pourrons transformer un plan quelconque en un plan vertical

  
Cas particuliers
La figure appartient à un plan de bout par rotation autour d'un axe de bout placé dans ce plan, nous pouvons définir la V.G de celle-ci

 

  • nous déterminons les traces du plan ABC ( PaQ')
  • la trace horizontale sert d'axe de rotation puisqu'elle est une droite de bout
  • en projection frontale les 3 points ( a',b',c') décrivent des arcs de cercle et se retrouvent confondus avec la ligne de terre en ( a'1 , b'1, c'1)
  • puis par ligne de rappel en ( a1 , b1, c1 ) ce qui représente le triangle ABC en V.G


 Nous pouvons comprendre l'opération similaire qui consiste à exécuter une rotation d'une figure appartenant à un plan vertical dans ce cas on utilise la trace frontale du plan comme charnière de rotation
Cette pratique nous permet d'envisager la technique du rabattement