|
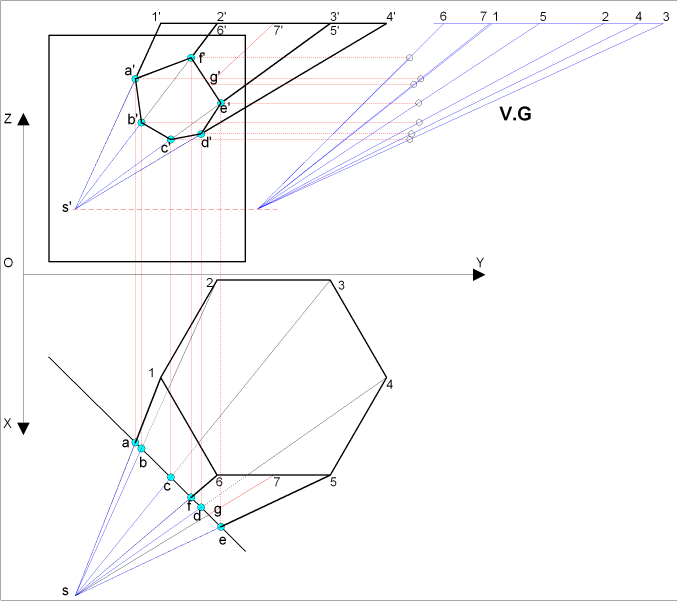
Soient les projections H et F d'une pyramide à
base pentagonale (pentagone régulier) coupée
par un plan vertical
- l'intersection en proj. F se définit par les lignes
de rappel des points (b,c,d,e
et r)
ce qui donne les points (b',c',d',e' et
r')
- pour le point ( a'), nous devons
choisir un frontale (f, f') du
plan S12 passant par le point (a)
définissant une droite parallèle
à ( (1'2' ) en proj.
F
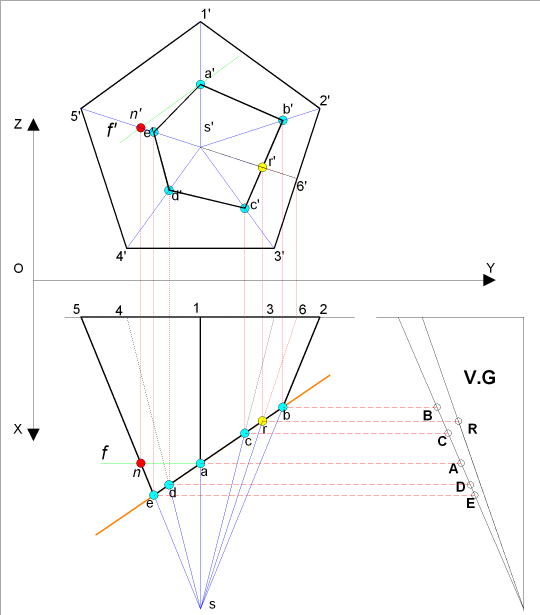
- toutes les arêtes ont même VG Þ( même
valeur en projection F et même différence d'éloignement)
- recherchons comme le montre le dessin ci-contre la VG de
S1 et de S6 ( ligne
d'assemblage choisi au milieu de (45)
)
- il suffit de porter l'ensemble des points (A,B,C,D,E,R)
sur la VG S1 puisque (sa / s1 =
SA /S1 ), nous sommes en possession de tous les éléments
pour développer
|
 |
![]()
![]()