![]()
![]()
![]()
![]()
Le plus souvent, nous placerons des génératrices dans le solide pénétrant (cône)
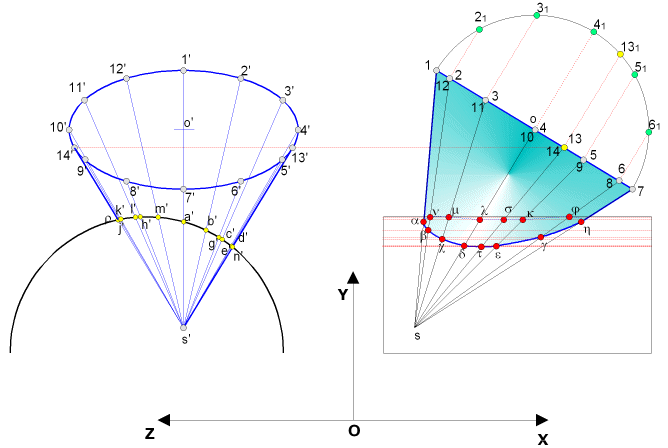 |
En épure
|
Cône
de révolution axe vertical -Cylindre de révolution axe frontal
Les axes des 2 solides ( non concourants), là aussi nous allons faire
passer des plans sécants par le sommet du cône de telle manière
à définir des génératrices dans le cylindre
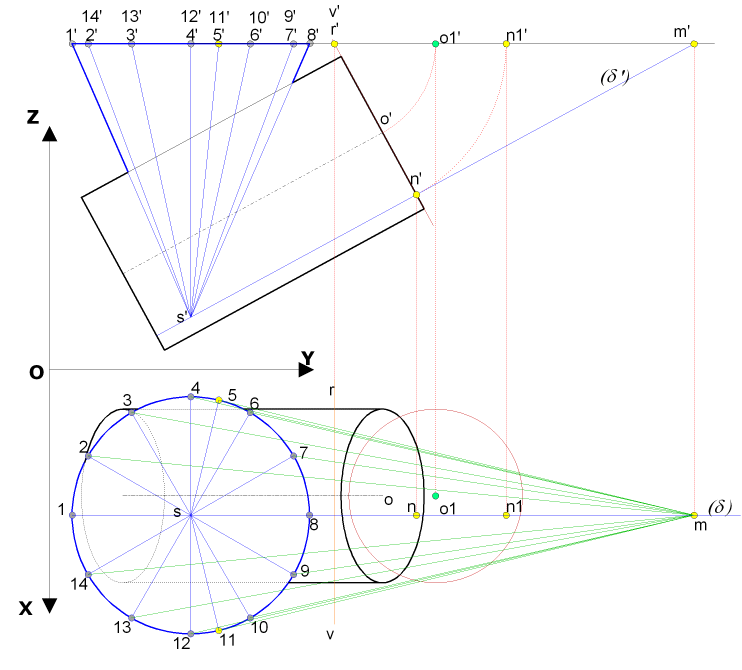 |
Nous savons que 2 droites parallèles définissent un plan
|
|
|
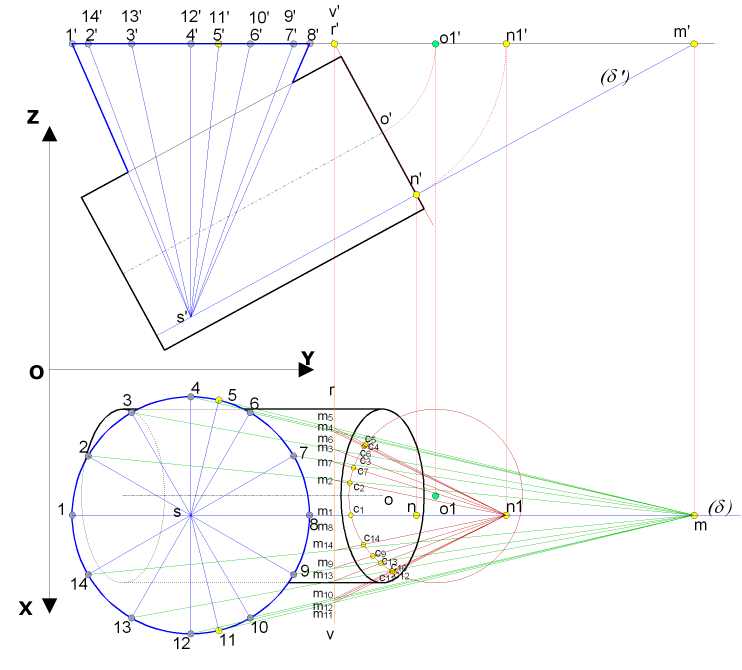 |
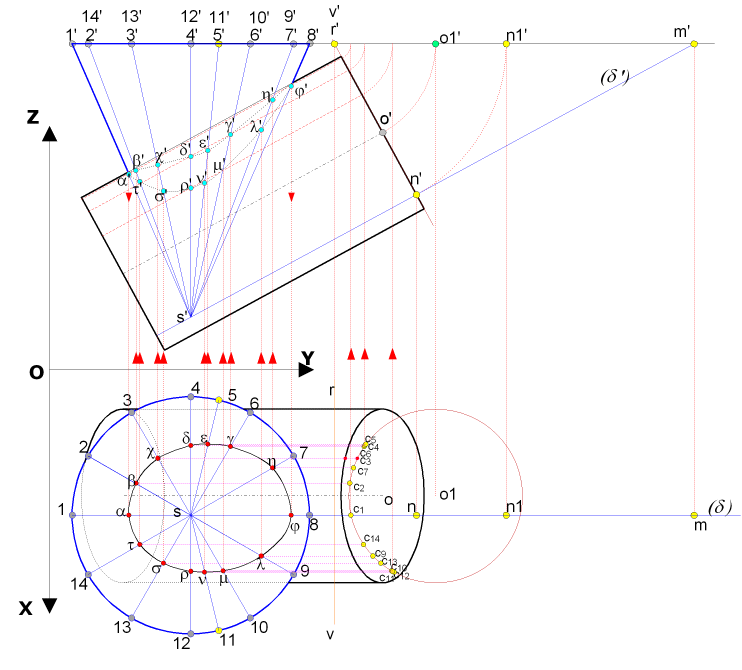 |
En épure
|
|
voir animation |
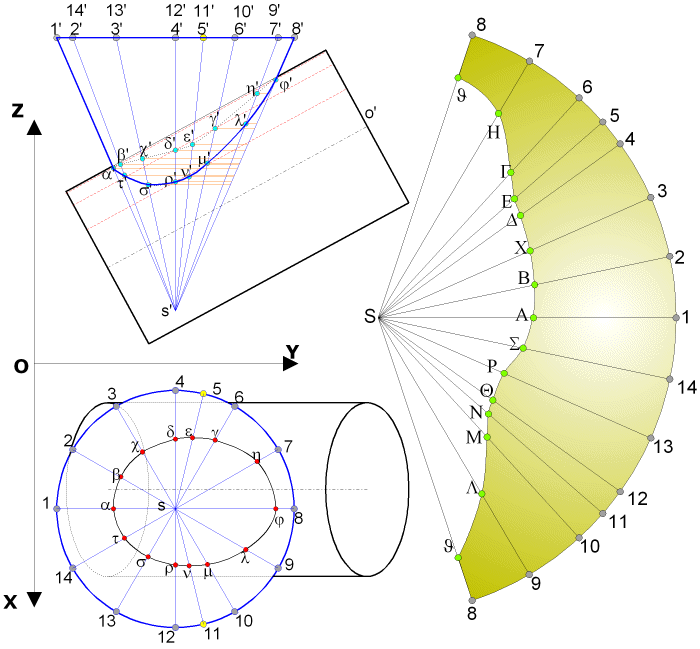 |
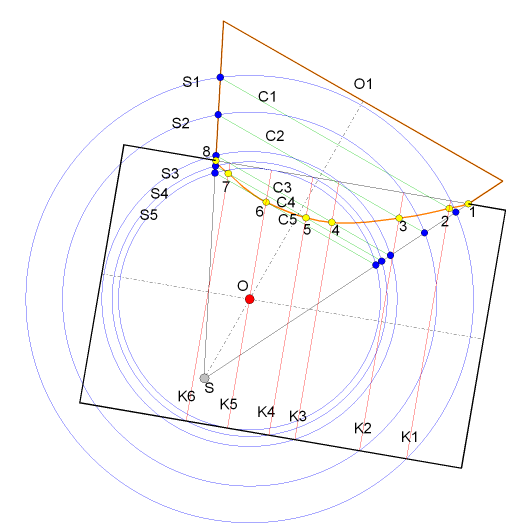 |
En épure
Attention les points déterminés sont doubles puisque notre problème présente un axe de symétrie |