Document sans titre

Définition / Méthode de recherche


Cercle - Triangle	Cercle - Rectangle	Cercle- Polygone rayon

Définition :
On dénomme surface dite "composée", le solide dont la surface latérale est constituée de plusieurs éléments, ces éléments étant une partie de surface développable tel que ( plan, cylindre , cône, etc...)

Animation de la recherche des plans tangents et détermination de la surface de raccordement

Plans tangents:
La recherche des plans tangents délimitant la surface latérale entre deux sections dans 2 plans concourants est la méthode choisie pour définir notre surface composée.

Déroulement de la recherche ci-dessus:

Prolongeons la droite CA jusqu'à sa rencontre avec le plan P contenant le cercle de centre O donnant le point Mac.
Procédons de même manière pour la droite CB .. on obtient le point Mbc dans le plan P
Ensuite pour la droite AB.... on obtient le point Mab dans le plan P
La droite Mab, Mbc,Mac est la droite d'intersection du plan P et du plan passant par le triangle ABC
Des points Mab, Mbc, Mac , nous traçons une tangente au cercle de centre O nous donnant respectivement les 3 points de tangence T1, T2, T3.
Traçons les surfaces planes de raccordement ABT1, BCT2, CAT3
Entre chacune des surfaces planes précitées nous obtenons dans ce cas des portions de surface conique définissant notre raccord entre le cercle et le triangle
Conclusion: Lorsque nous cherchons le raccordement de 2 bases non parallèles, il convient de déterminer la droite d'intersection des 2 plans contenant chacun une des bases, puis suivant la forme de celles-ci, faire passer le minimum de plans judicieusement choisi pour définir les plans tangents donnant soit des surfaces , soit des droites de raccordement pouvant appartenir à des portions de solides simples.

Exemple 1:Raccordement d'un cercle dans un plan horizontal et d'un triangle dans un plan de bout.

Notre raccord est dans une position privilégiée puisque la projection horizontale du cercle nous représente le cercle en VG.( constatation importante pour la facilité de la recherche de la tangente au cercle )

La démarche à suivre est la suivante:

déterminons la droite d'intersection des 2 plans contenant les 2 sections à raccorder ( droite de bout puisque intersection d'un plan horizontal avec un plan de bout )
traçons la droite (ab,a'b') jusqu'à sa rencontre avec la droite d'intersection des 2 plans soient les points ( m_ab,m'_ab)
faisons de même pour les 2 droites AC et CB nous donnant respectivement les points (m_ac,m'_ac; m_cb,m'_cb)
de ces points, traçons les tangentes au cercle qui donnent les points de tangence (t₁, t'₁, t₂,t'₂ , t₃, t'₃).
les surfaces triangulaires (abt₃,a'b't'₃, act₁, a'c't'₁, bct₂,b'c't'₂) nous définissent les surfaces planes de notre raccordement.
les surfaces entre les plans sont des portions de surfaces coniques

déterminons un nombre de génératrices en divisant le cercle entre chaque point ( T1, T2, T3)
- Sommet A : points 11, 12, 1, 2, 3
- Sommet B : points 5, 6, 7, 8
- Sommet C : points 9, 10
choisissons un point D entre A et C pour prendre comme droite d'assemblage D T1
recherchons les différentes VG des droites en utilisant comme principe : projection horizontale et différence de cotes

Pour le développement nous reportons comme pour les surfaces coniques les écarts entre chaque pied de génératrices, il est conseillé de contrôler par exemple à chaque 1/4 de cercle, la longueur de la transformée sachant que la corde ne sous-tende pas la même courbure.

Vraies grandeurs des génératrices de sommet C

Vraies grandeurs des génératrices de sommet A

Vraies grandeurs des génératrices de sommet B

Développement tracé intérieur

Exemple 2:Raccordement d'un rectangle dans un plan frontal et d'un cercle dans un plan vertical.

a) Solution par rotation

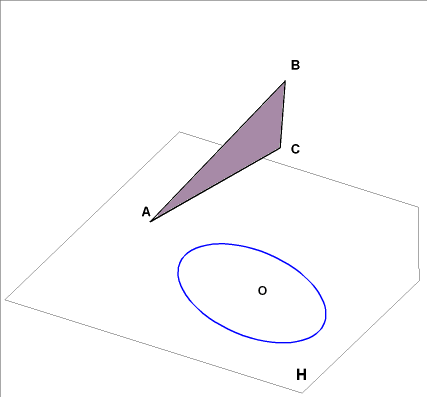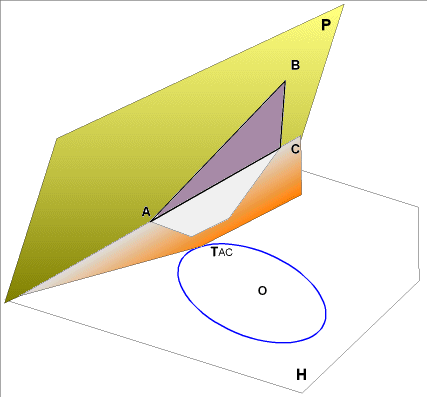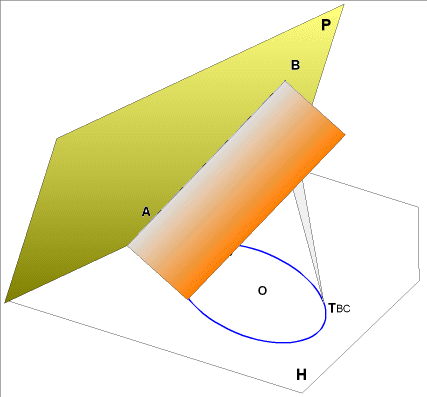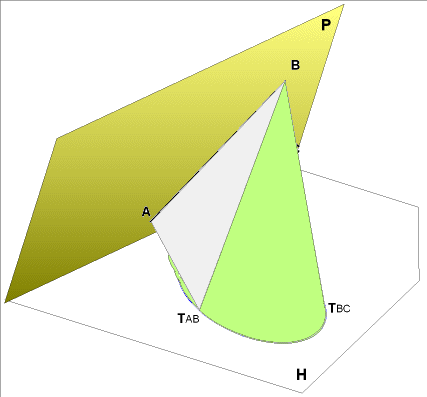
Dans ce cas la section circulaire n'étant pas en VG dans une projection

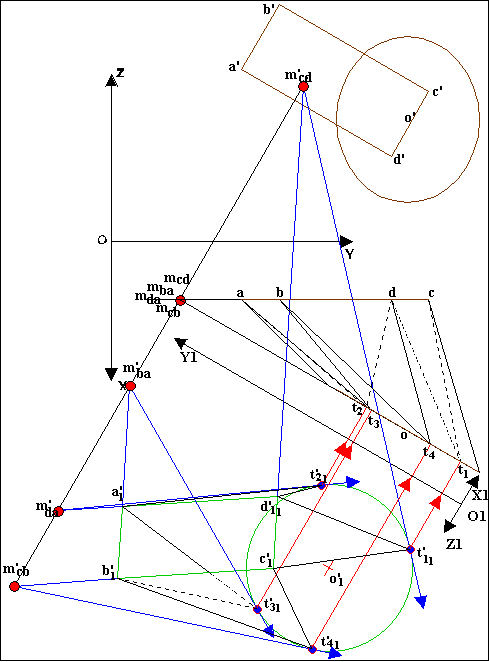
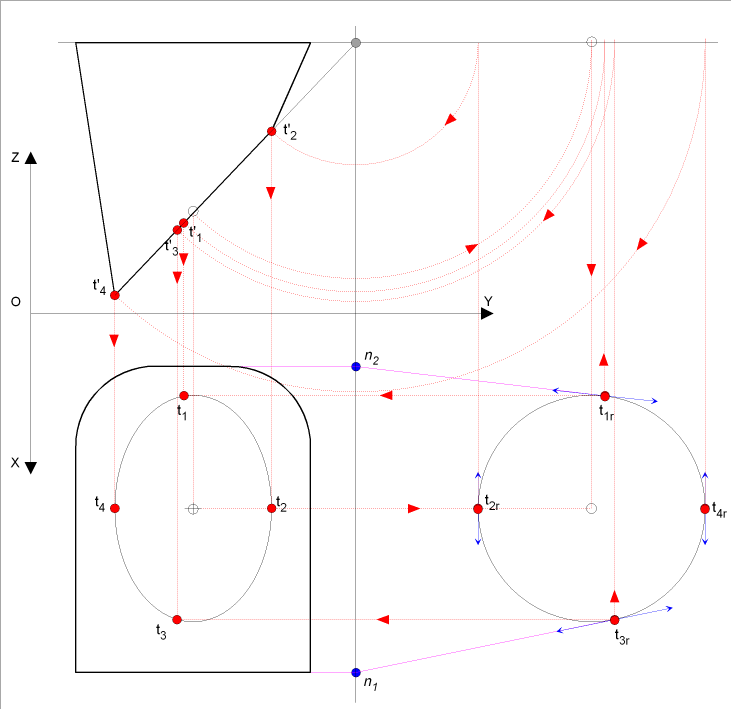
nous nous proposons d'effectuer une rotation (axe Þ intersection des 2 plans) de celle-ci dans le plan de la surface rectangulaire pour 2 raisons:
1. Il est plus facile de recherche une tangente à un cercle qu'à une ellipse
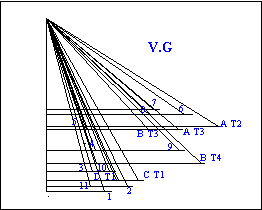
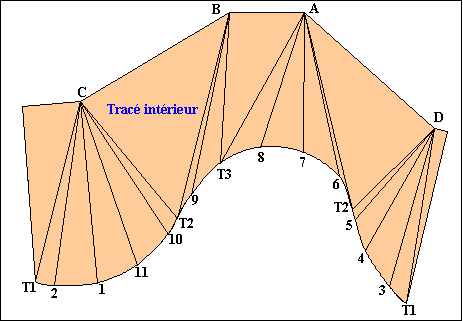
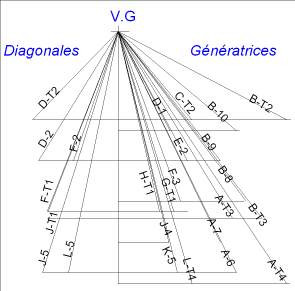
2. Nous aurons besoin pour le développement de connaître les écarts entre chaque pied de génératrices sur la base circulaire.
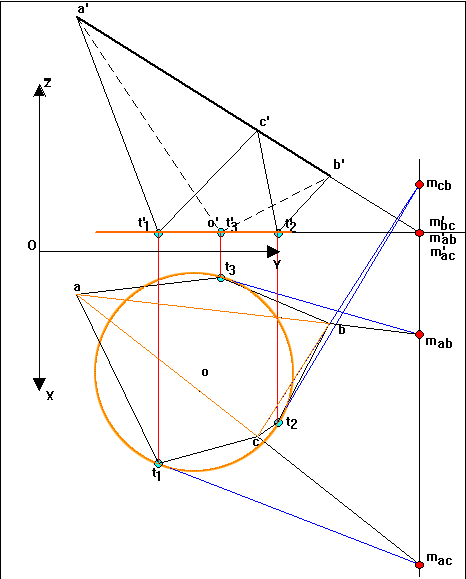
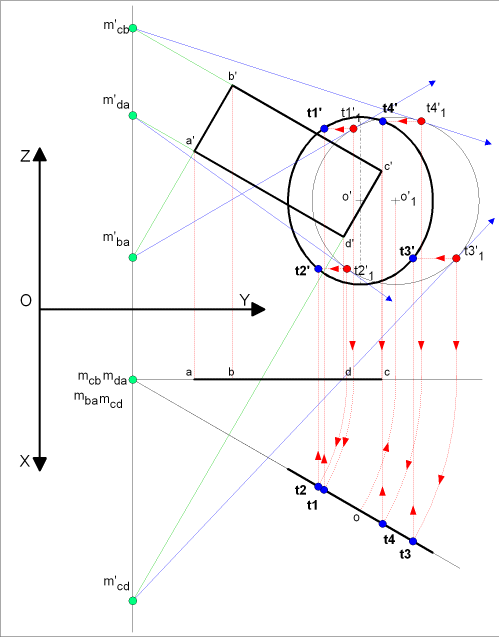
déterminons la droite d'intersection des 2 plans ( droite verticale )
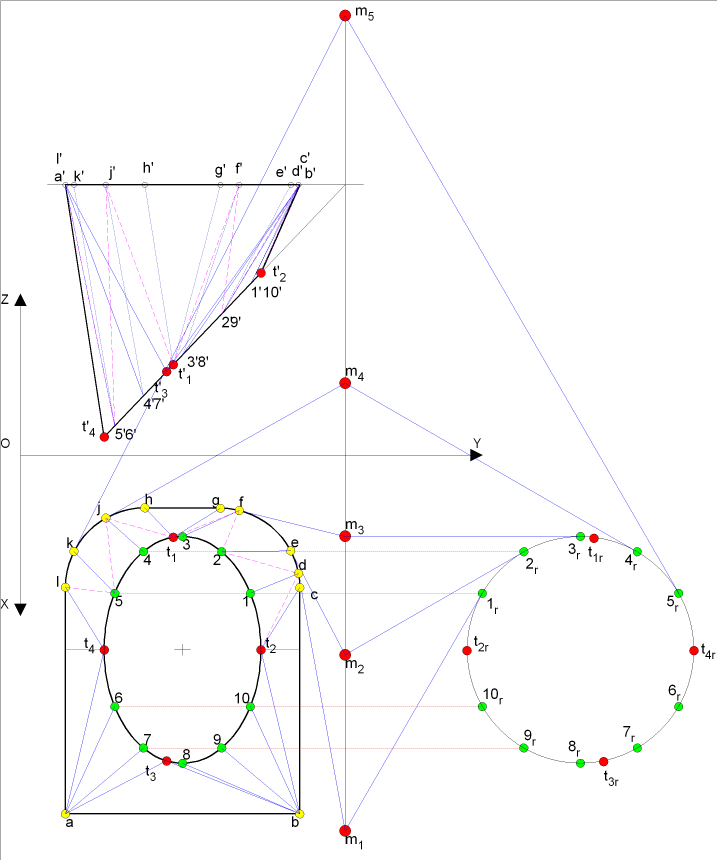
en PF, prolongeons les droites ( b'c', c'b',c'd',d'a') nous donnant les points ( m' _ba, m' _da, m' _cb, m' _cd) qui nous permettent de tracer les tangentes respectives au cercle rabattu de centre ( o'₁) Þ soient les points obtenus ( t'1₁, t'2₁, t'4₁, t'3₁,)
nous les reportons sur l'ellipse (t'₁, t'₂, t'₄, t'₃, ) et en PH pour nous donner les points (t₁, t₂, t₄, t₃, )

déterminons un nombre de génératrices en divisant le cercle entre chaque point ( T1, T2, T3,T4)
- Sommet A : points 6, 7, 8
- Sommet B : points 9
- Sommet C : points 10, 11, 1, 2
- Sommet D : points 3, 4, 5
choisissons un point E entre D et C pour prendre comme droite d'assemblage E T3
recherchons les différentes VG des droites en utilisant comme principe : projection frontale et différence d'éloignements

b) Solution par changement de plan

Dans ce cas la section circulaire n'étant pas en VG dans une projection nous nous proposons d'effectuer un changement de projection frontale avec un nouveau repère OX₁Y₁Z₁tel que OY₁ soit parallèle à la section circulaire, nous donnant dans la nouvelle projection frontale le cercle en VG et la surface rectangulaire en raccourci partiel, nous nous retrouvons comme dans l'exemple 1 pour effectuer les diverses recherches.

Exemple 3 :Raccordement entre une section circulaire dans un plan de bout et une section polygonale avec rayons dans un plan horizontal.

Commençons par déterminer la droite d'intersection des 2 plans qui est en l'occurrence une droite de bout,
effectuons un rabattement du plan contenant le cercle autour de cette droite de bout tel que le plan soit dans le même que celui du polygone
la recherche des plans tangents se fait en commençant par les parties droites de la section polygonale en prolongeant les droites jusqu' à la droite d'intersection , nous donnant les points sur la droite d'intersection (n₁,n₂,) pour les 2autres droites étant données qu'elles sont parallèles à la droite d'intersection , les tangentes au cercle sont aussi parallèles à la droite d'intersection(t₂, t₄,).
traçons les tangentes au cercle rabattu donnant les points (t₃, t₁,) que l'on reporte ensuite sur l'ellipse et sa projection frontale

les plans tangents définissent 4 surfaces triangulaires ainsi entre chaque plan des surfaces développables
- pour le sommet A une portion de surface conique
- pour le sommet B une portion de surface conique
- pour les 2 autres surfaces il nous faut définir des génératrices en utilisant la méthode des plans tangents
- nousdéfinissons des points sur le cercle rabattu entre chaque point ( t1r, t2r,t3r, t4r) de chacun des points ( 5r, 4r,3r,2r, 1r) nous faisons passer une tangente au cercle qui coupe la droite d'intersection des 2 plans suivant les points respectifs( M5, M4, M3, M2, M1); de chaque point obtenu il suffit de chercher la tangente au rayon, ainsi on détermine les points:
  - d Þ 1
  - e Þ 2
  - f Þ 3
  - j Þ 4
  - k Þ 5
construisons les projections frontale et horizontale de l'ensemble des points.
traçons les génératrices nécessaire au développement ainsi que les "diagonales" en triangulation
partageons le solide en 2 parties pour le développer
définissons les VG de l'ensemble des droites par le principe ( projection horizontale et différence de cotes). Pour plus de clarté séparons les génératrices des "diagonales"

Les 1/2 développements (tracé intérieur) ne présentent aucune particularité , pensons toutefois à bien reporter les écarts entre les points sur le cercle rabattu ( VG)